未整理

1
2
Cholesky Factorization
Covariance Matrix
Fibonacci Number
Generating function
Graph Node and Edge
QR factorization
Reflexive Colsure
Relation
Similar Matrix
SVD
Transition Matrix

Fibonacci / Biomial coefficient identity

\( \begin{pmatrix} n \\ m \end{pmatrix} = \begin{pmatrix} n-1 \\ m \end{pmatrix} + \begin{pmatrix} n-1 \\ m-1 \end{pmatrix} \)
\( \frac{d}{dx}\ln x=\frac{1}{x} \)
\( \frac{d}{dx}e^x=e^x \)

lb \( lb_2x \)
ln \( ln_ex \)
lg \( lg_{10}x \) or \( lg_2x \)


\( \frac{d}{dx}(f(x)^{g(x)}) = g'(x) \cdot \frac{d}{dx}(f(x)^{g(x)}) \)
\( \Rightarrow \frac{d}{dx}e^{g(x)} = g'(x)\cdot e^{g(x)} \)

L'Hôpital's rule

\( \lim\frac{f(x)}{g(x)} = \lim\frac{f'(x)}{g'(x)} \)

limit

\( \lim_{n\rightarrow \infty}(1+\frac{1}{n})^n = e \)
\( \forall k,a,b\in R^+, \)
\( (\log_an)^b =o(n^k) \)

Geometric series

\( c\neq 1,c\in R, a_n=ca_{n-1}\;\;, a_1+a_2+\dots+a_n= a_1\frac{c^n-1}{c-1} = a_1\frac{1-c^n}{1-c} \)
** \( 0< c< 1, c\in R, a_n=ca_{n-1}\;\;, a_1+a_2+\dots+a_n= \frac{a_1}{1-c} \)

\( \displaystyle\sum_{i=0}^{\infty}n\cdot a^i = \frac{n}{1-a} ,\; 0< a < 1 \)

Log

\( \log_ba=\frac{1}{\log_ab} \)
\( \log_ax=\frac{\log_bx}{\log_ba} \)
\( b^{\log_bx}=x \)
\( b^{\log_ax}=x^{\log_ab} \)
\( \lg n \equiv \log_2n \)
reference: 洪捷-演算法

\( \log_{a}^{b}=-\log_{\frac{1}{a}}^{b} \)

time complexity

harmonic series

\( H_n= \frac{1}{1}+ \frac{1}{2}+ \dots \frac{1}{n} = \Theta(\ln n) \)
 proof
\( H_n=\int_1^n\frac{1}{x}dx \)
\( =\ln n - \ln 1 \)
\( =\log_e n - \log_e 1 \)
\( =\ln n \)


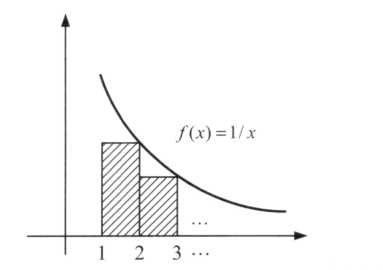
\( \frac{1}{2}+ \frac{1}{3}+ \dots+ \frac{1}{n} =T(n)-1 \)
\( \rightarrow T(n)-1 < \ln n \)
\( \rightarrow T(n)< \ln n-1 \leq 2\ln n, \forall n\geq 3 \)
\( \rightarrow T(n)=O(\ln n) \)


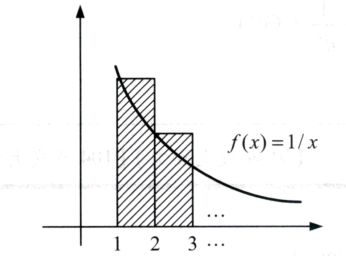
斜面面積\( T(n) \):大於 \( \ln n \)
\( \rightarrow T(n)>\ln n \)
\( \rightarrow T(n) = \Omega(\ln n) \)

\( \because [T(n)=O(\ln n)] \cap [T(n)=\Omega(\ln n)] \)
\( \therefore T(n)=\Theta(\ln n) \)

\( \log(n!)= \Theta(n\lg n) \)

\( \forall k,a,b\in R^+, \)
\( n^k = \omega(\log_a^bn) \)
\( x^n-a^n \)
\( = (x-a)(x^{n-1}+x^{n-2}a+\dots+xa^{n-2}+a^{n-1}) \)
\( \sum_{k=1}^{n}n= \frac{n(n+1)}{2} \)

\( \sum_{k=2}^{n}n= \frac{n(n+1)}{2}-1 \)

\( \sum_{k=2}^{n}n= \frac{n(n-1)}{2} \)

\( \sum_{k=1}^{n}k^2 = \frac{n(n+1)(2n+1)}{6} \)
\( 2^k+ 2^{k-1}+ 2^{k-2}+ \dots +2+1 \)
\( = 2^{k+1}-1 \)
\( \frac{n^2-n}{2} = \begin{pmatrix} n \\ 2 \end{pmatrix} \)

\( \frac{n^2-n}{2} = \frac{n(n-1)}{2} = \frac{n!}{(n-2)!2!} \)
\( p \rightarrow q \equiv \neg p \vee q \)
\( \cos\angle{ABC} = \frac{\vec{BC}\vec{BA}}{\lVert BC\rVert \lVert BA\rVert} \)
\( 0\leq r,\)
\( 0\leq n,\)
\( r\leq n, \) \[ \begin{pmatrix} n+1 \\ r+1 \end{pmatrix} = \sum_{i=r}^{n} \begin{pmatrix} i \\ r \end{pmatrix} = \sum_{i=r+1}^{n+1} \begin{pmatrix} i-1 \\ r \end{pmatrix} \]
Suppose that \(V\subseteq F\),   \(u,v\in V\)
\( <\cdot , \cdot > \) means inner product.
def.
\( <f ,g>=\frac{1}{2}\int_{-1}^{1}f(x)g(x)dx \)
or
\( <f ,g>=\int_{0}^{1}f(x)g(x)dx \)


Cauchy-Schwarz inequality
\( |<u ,v>| \leq \lVert u\rVert \lVert v\rVert \)

\( \Rightarrow -1\leq \frac{<u ,v>} { \lVert u\rVert \lVert v\rVert } \leq 1 \)

Triangle inequality
\( \lVert u+v\rVert \leq \lVert u\rVert + \lVert v\rVert \)

Taylor series

\[ e^x = \sum_{i=0}^{\infty} \frac{x^i}{i!} =1 +\frac{x^1}{1!} +\frac{x^2}{2!} +\dots +\frac{x^n}{n!} +\dots \]
orthonormal set 一定是independent的。
orthognal set 不一定為independent，因為它可能包含零向量。