Definition expression(Root Tree)

There have a tree(Rooted tree).
It is directed.
\( \text{Root} = \text{parent} = R= T_0 \)
\( \text{subtree} = \text{child} = \{T_n \;|\; \forall n\in N, n\neq 0\} \)

Expression
Tree= \( (R,T_1,T_2,\dots, T_n) \)

parent / father

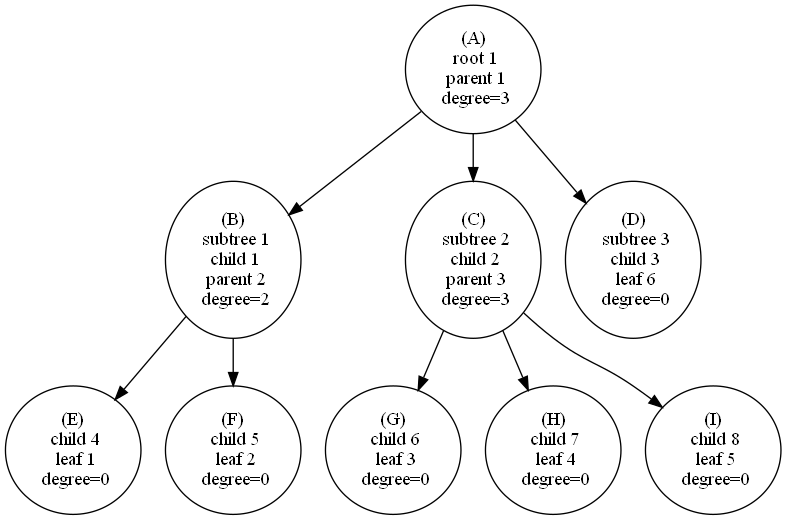
A is parent of {B, C, D}.
B is parent of {E, F}

child / son / subtree

B, C, and D are child from A.

ancestor

All root from this node.
A and B are ancestor from E.

descendant

Except A from the tree, all nodes are descendant from A.

brother / sibling

C is brother from B.
F, G, H, and I are brother from E.

leaf

Degree is zero.

level | height / depth

Example from graph.
level 1 = A.
level 2 = {B, C, D}
level 3 = {E, F, G, H, I}
depth = 3

空間利用

假設
node的個數為n
每一個node建立時，需要k個指標空間。
一共會創造nk個指標空間。
那樹的形狀如果是skewed tree。
實際有使用的指標空間為(n-1)
沒使用的指標空間為nk-(n-1)個。
所以利用以下方法可以避免指標空間的浪費。
  1. generalized list
  2. left-child right-sibling
  3. binary tree

Generalized list

expression

Create a tag to determine tree or leaf.
\( T=(R,T_1,T_2,\dots,T_n) \)
\( T_1 = (B,\; E,F) \)
\( T_2 = (C,\; G,H) \)
\( T_3 = D \)
\( \Rightarrow (\;A,\;(B,\;E,F),\;(C,\;G,H),\;D\;) \)

code(c)


解釋
箭頭為nextLink指向。
\( A \rightarrow (B,E,F) \rightarrow (C,G,H) \rightarrow D \rightarrow \text{Null} \)
\( B \rightarrow E \rightarrow F \rightarrow \text{Null} \)
\( C \rightarrow D \rightarrow H \rightarrow \text{Null} \)
tag為true表示連結tree，那node就選treeLink，
表達式裡指向遇到刮號就選treeLink。
 Original tree
Images of generalized list
\( \Rightarrow (\;A,\;(B,\;E,F),\;(C,\;G,H),\;D\;) \)

Left-child Right-Sibling

As title.

Order of son(subtree) is not important.

code(c)

 Original tree
Left-Child Right-Sibling

Binary tree

Order of subtree is not important.

Order of subtree of binary tree is important.

Graph as left-child right-sibling,
but there is different from left and right tree to assign.
Left and right tree need to be defined clearly. .

code(c)

 Different binary tree