Recurrence Relation是為利用自身函數來表達自己函數的方法。
例如:
費式數列(Fibonacci number)
\( F(n)=F(n-1)+F(n-2) \)

Substitution Method(替代法)

策略
  1. 經驗法則猜結果(asymptotic)
  2. 用mathematic induction找出常數(asymptotic的邊界條件)，來證明此猜測是對的。

Question

Determine asymptotic from \( T(n)=2T(\lfloor \frac{n}{2} \rfloor)+n, \; T(1)=1 \)

ans

Guess \( T(n)=O(n\lg n)\)
Let \( \exists c\in \mathbb{R} \rightarrow T(n)\leq cn\lg n \)

Mathematic Induction
Suppose that \( T(\lfloor \frac{n}{2}\rfloor) \leq c\lfloor \frac{n}{2} \rfloor \lg \lfloor \frac{n}{2} \rfloor \) existed.

\( \Rightarrow T(n) \leq 2\cdot c\lfloor \frac{n}{2} \rfloor \lg \lfloor \frac{n}{2} \rfloor + n \)
\( \leq 2\cdot c\frac{n}{2} \lg \frac{n}{2} +n \)
\( = cn(\lg n-\lg 2)+n \)
\( = cn\lg n - cn\lg 2 +n \)
(這裡已經可以看出式子在n很大時，\( n\lg n \)為主導。)
when \( c=2,\;n\geq 2 \rightarrow T(2)=2T(1)+2=4\leq 2\cdot 2\lg 2 \) existed.

Recursion-tree Method(遞迴樹法)

母問題分解成多個子問題，然後子問題當成母問題再繼續分解成多個子問題，直到子問題不能再被分解為止。

策略

  1. 展開recursion relation
  2. 從母問題分解出來的子問題，那層的子問題的加總，可當作這層的成本花費。
  3. 每層成本加起來，可得到整顆樹的花費。

Question

Give asymptotic tight bound for \( T(n)=T(\frac{n}{2})+T(\frac{n}{4})+T(\frac{n}{8})+n \) (assume that \( T(n) \) is constant for sufficiently small \( n \).)

ans

將\( T(n) \)展開得
ex_1
(第一層為n，是\( T(n)=\dots + {\color{blue} n} \))
再將子問題展開得
ex_2
(樹的最左邊層數較多，最右邊層數越少。)
(最右邊直的那排為每層的花費)

則總花費為
\( T(n)=n+\frac{7}{8}n+\frac{49}{64}n+\dots+\text{ leaf } \)
當n夠大時，是前面幾項在主導。

計算Big-Oh
\( \Rightarrow T(n)\leq n+\frac{7}{8}n+\frac{49}{64}n+\dots = \frac{n}{1-\frac{7}{8}} =8n \)
\( \Rightarrow T(n)=O(n) \)

計算Omega
\( n\leq T(n)=n+\frac{7}{8}n+\frac{49}{64}n+\dots+\text{ leaf } \)
\( \Rightarrow T(n) = \Omega(n) \)

\( \therefore T(n)=\Theta(n) \)

Question

Given tight asymptotic bounds for \( T(n)=T(n/3)+T(2n/3)+n \)

ans

Determine \( \Theta \).
展開\( T(n) \)為
ex2_2
從樹的花費可得知\( T(n) \)的總花費，
為\( T(n) = \overbrace{n+n+\dots+\text{ leaf}}^{\text{項目個數為最長樹高層數}}. \)
從上圖的樹可知道\( n/3 \)那條分支最先分完，\( 2n/3 \)最後分完，那就可以知道只要有分支分完，那層的花費加總就不會是\( n \)，就可用來比大小，算出\( O \)和\( \Omega \)。

計算Big-Oh:
\( T(n)=n+n+\dots+\text{ leaf} \leq \text{最長樹高}\times n \)
\( \Rightarrow n \rightarrow \frac{2n}{3} \rightarrow \frac{4n}{9} \rightarrow \frac{8n}{27} \dots T(1) \)
這裡有個想法，n每次都乘\( \frac{2}{3} \)直到變成\( T(1)=1\)
那樹高為，假設為\( h \)
\( n\cdot (\frac{2}{3})^{h}=1 \)
\( n=(\frac{3}{2})^{h} \)
取log
\( \log_{\frac{3}{2}} n = h\log_{\frac{3}{2}}\frac{3}{2} =h \)
\( \Rightarrow T(n) \leq (\log_{\frac{3}{2}} n)\cdot n=O(n\lg n) \)
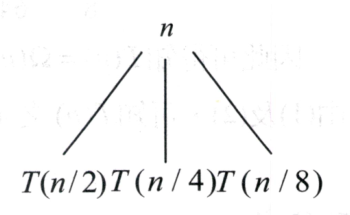
Hint
log之間比較order時，不同的底並不影響，
因為可以用換底公式換成一樣的底。
計算Omega: 找樹高最短的
\( \Rightarrow n\rightarrow \frac{n}{3}\rightarrow \frac{n}{9}\rightarrow \dots T(1) \)
假設樹高為h
則
\( n\cdot(\frac{1}{3})^{h}=1 \)
\( n=3^h \)
\( h=\log_{3}n \)

\( \Rightarrow n\cdot(\log_3n)\leq T(n) \)
\( \Rightarrow T(n)=\Omega(n\lg n) \)

\( \therefore T(n)=\Theta(n\lg n) \)

定理

由上面兩題得到一個定理。
Given positive constants: \( c_1,c_2,\dots,c_k,c' \),
assume that
\( T(n)\leq T(c_1n)+T(c_1n)+\dots T(c_kn)+c'n. \)
If these constant:
  1. \( c_1+c_2+\dots+c_k< 1, \text{ prove } T(n)=O(n) \)
  2. \( c_1+c_2+\dots+c_k=1, \text{ prove } T(n)=O(n\log n) \)
因為是呼叫自身函數，所以存在一個倍數關係。假設這個關係為r
令 \( r=c_1+c_2+\dots+c_k \),且\( T(n)=T(c_1n)+T(c_2n)+\dots +T(c_kn)+c'n \)
展開recursion-tree為
recursion_tree_proof
  1. 若\( r=c_1+c_2+\dots +c_k < 1 \)
    則
    \( T(n)=T(c_1n)+T(c_2n)+\dots +c'n \)
    \( T(c_1n)=T(c_1c_1n)+T(c_2c_1n)+\dots +T(c_kc_1n)+{\color{red}c_1c'n} \)
    \( T(c_2n)=T(c_1c_2n)+T(c_2c_2n)+\dots +T(c_kc_2n)+{\color{red}c_2c'n} \)
    \( \vdots \)
    \( T(c_kn)=T(c_1c_kn)+T(c_2c_kn)+\dots +T(c_kc_kn)+{\color{red}c_kc'n} \)
    \( \rightarrow c_1c'n+c_2c'n+\dots c_kc'n = rc'n \) (這個為\( c'n \)下一層的花費)

    最後都展開後
    \( T(n)=\text{ leaf } + \text{ leaf } +\dots +r^2c'n+rc'n+c'n\)
    整理式子(倒過來寫
    \( T(n)= c'n+rc'n+r^2c'n+\dots +\text{ leaf } + \text{ leaf }\)
    這是有限項的式子，如果無限加正數一定會比這個大(就算一直加的數是接近無限小的正數)。
    所以得到
    Hint
    \( 0< c< 1, a_n=ca_{n-1} \rightarrow \displaystyle\sum_{i=1}^{\infty}a_i=\frac{a_1}{1-c} \)

    \( T(n)\leq c'n+rc'n+r^2c'n+ \dots =\frac{c'n}{1-r}\)
    \( \therefore T(n)=O(n) \)

    計算Omega:
    如果樹只有一層，很明顯為
    \( an\leq T(n),\; a\in R \)
    \( \therefore T(n)=\Omega(n) \)

    \( \because T(n)=\Omega(n)\cap T(n)=O(n)\)
    \( \therefore T(n)=\Theta(n) \)
  2. 若\( r=c_1+c_2+\dots +c_k=1 \)
    \( T(n)=c'n+c'n+\dots +c'n =\text{樹高}\cdot c'n\)
    樹高\( =\Theta(\log n) \)
    \( T(n)=(\log n)\cdot c'n=\Theta(n\log n) \)
    樹高證明
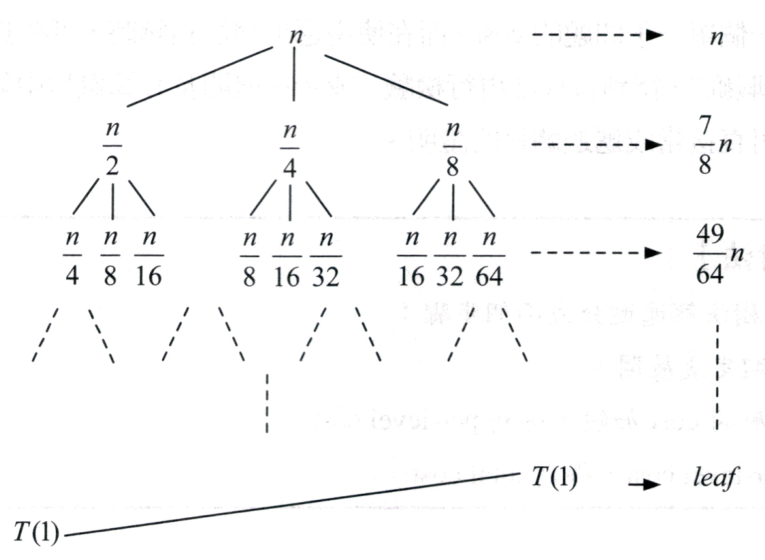
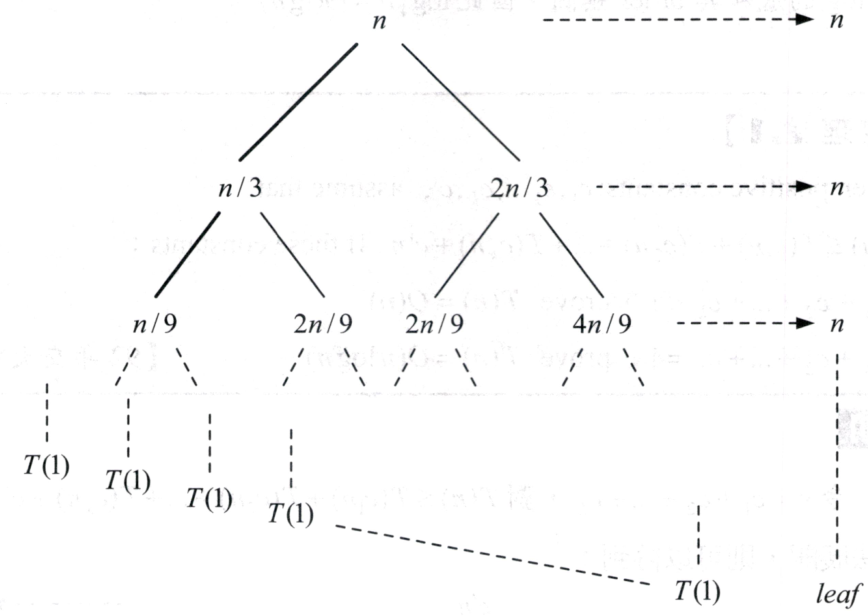
    proof:

    計算樹高Big-Oh:
    最長子樹的倍數關係為t
    則
    \( n\rightarrow tn\rightarrow t^2n\rightarrow \dots \rightarrow 1 \)
    \( n\cdot t^{\text{樹高}}=1 \)
    \( n=(\frac{1}{t})^{\text{樹高}} \)
    \( \log n = \log_{\frac{1}{t}}(\frac{1}{t})^{\text{樹高}} \)
    \( \text{樹高}=\log_{\frac{1}{t}} n \)
    \( \therefore \text{樹高}=O(\log n) \)

    計算樹高Omega:
    計算最短子樹，其倍數關係為s
    則
    \( n\rightarrow sn\rightarrow s^2n\rightarrow \dots \rightarrow 1 \)
    \( n\cdot s^{\text{樹高}}=1 \)
    \( n=(\frac{1}{s})^{\text{樹高}} \)
    \( \log n = \log_{\frac{1}{s}}(\frac{1}{s})^{\text{樹高}} \)
    \( \text{樹高}=\log_{\frac{1}{s}} n \)
    \( \therefore \text{樹高}=\Omega(\log n) \)


    \( \log \)的底數可由換底公式變成一樣的，然後原來的底數會變成係數，在比較時間複雜度時，並不會考慮係數，因為n夠大，係數不能構成式子的主導權，主導權在最高次方的變數身上。
    \( \because \text{樹高}=O(\log n) \cap \text{樹高}=\Omega(\log n) \)
    \( \therefore \text{樹高}=\Theta(\log n) \)

Master-theorem Method(老大定理)

\( a\geq 1, b> 1, \forall a,b\in R \)
\( f:f(n) \) (意思\( f(n) \)為一函數
\( T(n) \geq 0 \rightarrow T(n)=aT(\frac{n}{b})+f(n)\)
有三種情況

  1. \( \exists \varepsilon ( \underline{(\varepsilon> 0)}\wedge \underline{f(n)=O(n^{\log_{b}a-\varepsilon})} \rightarrow \underline{T(n)=\Theta(n^{\log_{b} a})} ) \)

  2. \( \forall k ( \underline{(k\geq 0)}\wedge \underline{f(n)=\Theta(n^{\log_{b} a}\lg^k n)} \rightarrow \underline{T(n)=\Theta(n^{\log_b a}\lg^{k+1}n)} ) \)

  3. \( \exists\epsilon\exists c ( \underline{(\epsilon > 0)}\wedge\underline{(c < 1)}\wedge \underline{f(n)=\Omega(n^{\log_b a+\epsilon})} \wedge \underline{a\times f(\frac{n}{b})\leq cf(n)} \rightarrow \underline{T(n)=\Theta(f(n))} ) \)
判斷master theorem使用時機 (其一則可)
  1. \( (n^{\log_b a} \) \( \;/\; \) \( f(n)) \) \( \geq \) \( n^{\epsilon} \)
  2. \( ( f(n)\;/\; n^{\log_b a} ) \geq \lg^k n \)
    討論\( \lg^k n \)計算註解
    假設\( f(n)> n^{\log_ba} \)
    那就可以用\( ( f(n)\;/\; n^{\log_b a} ) \geq \lg^k n \) 判斷，接著是判斷\( k \)是否\( \geq 0 \)
    \( ( f(n)\;/\; n^{\log_b a} ) = n^c,\; c> 0 \)
    \( \Rightarrow n^c=\lg^k n \)
    取\( \log_{\lg n} \)
    \( \Rightarrow \log_{\lg n} n^c = \log_{\lg n} \lg^k n = \log_{\lg n} (\lg n)^k =k \)
    討論\( \lg n \):
    \( n \)是一個很大的數\( \lg \)底數是2，那他的值一定會大於1，如果\( \log \)的底數是分數的話出來的值會是負數，就不符合\( k\geq 0 \)

    改寫為
    \( \log_{\lg n} (\frac{f(n)}{n^{\log_b a}})=k\geq 0 \)
    判斷\( k \)值     		\( \forall n\forall c \)(\( (n\geq 1) \wedge (c>0) \) \( \rightarrow (n^c > 1)) \)

    \( \log_{\text{大於1的某數}}\text{大於1的某數}> 0 \)

Question

Please resolve the following recurrence relations.

exercise

\( T(n)=8T(\frac{n}{2})+n^2 \)

ans

\( a=8, b=2, f(n)=n^2 \)
\( \log_2 8 = 3 \Rightarrow n^3 \)
when \( \epsilon = 1 \),
checking \( n^3 / n^2 \geq n^1 \).
By Master theorem.
\( T(n) = \Theta(n^3) \)

exercise

\( T(n)=4T(\frac{n}{2})+n^3 \)

ans

\( a=4,\; b=2\; f(n) = n^3 \)
\( n^{\log_ba}= n^{2} \)
\( f(n)> n^{\log_ba} \)

checking
\( \log_{\lg n}\frac{f(n)}{n^{\log_ba}}\geq 0\rightarrow \)ok, 符合\( k\geq 0 \)
取 \( k= \log_{\lg n}n \)
By master theorem (3)
Hint
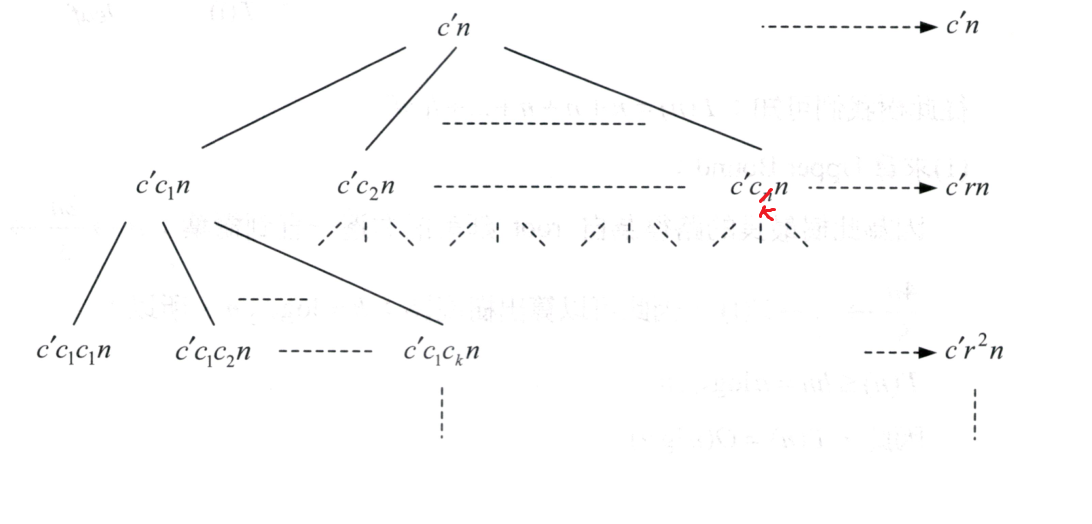
找到\( \varepsilon> 0 \)和\( c< 1 \)使得滿足 \( f(n)=\Omega(n^{\log_ba+\varepsilon}) \cap af(\frac{n}{b})\leq cf(n) \)
則\( T(n)=\Theta(f(n)) \)

\( f(n)= \Omega(n^{\log_24+\varepsilon}) \cap 4f(\frac{n}{2})\leq cf(n) \)
代\( f(n)=n^3 \)
\( \Rightarrow n^3= \Omega(n^{\log_24+\varepsilon}) \cap 4(\frac{n}{2})^3\leq cn^3 \)
\( \Rightarrow n^3= \Omega(n^{2+\varepsilon}) \cap 4(\frac{n^3}{8})\leq cn^3 \)
取 \( \varepsilon=1, \; c=\frac{1}{2} \)
得
\( T(n)=\Theta(n^3) \)

exercise

\( T(n)=4T(\frac{n}{2})+n^2\lg n \)

ans

\( a=4,\;b=2,\; f(n)=n^2\lg n \)
\( n^{\log_ba} = =n^{2} \)
\( k=\log_{\lg n}\frac{n^2\lg n}{n^2}=1 \)
By Master theorem (2)
\( f(n)=\Theta(n^{\log_ba}\lg^kn) \rightarrow \Theta(n^{\log_ba}\lg^{k+1}n) \)
\( \Rightarrow f(n)=\Theta(n^2(\lg n)^1) \rightarrow \)滿足
所以
\( T(n)=\Theta(n^2\lg^2n) \)

exercise

\( T(n)=2T(\frac{n}{2})+n \)

ans

\( a=2,\;b=2,\;f(n)=n \)
\( k=\log_{\lg n}\frac{f(n)}{n^{\log_ba}} =\log_{\lg n}\frac{n}{n}=0 \)

By master theorem (2)
\( f(n)=\Theta(n^{\log_ba}\lg^kn) \rightarrow T(n)=\Theta(n^{\log_ba}\lg^{k+1}n) \)

\( f(n)=n=\Theta(n^1\lg^0n)=\Theta(n) \)
\( \rightarrow T(n)=\Theta(n\lg n) \)

exercise

\( T(n)=3T(\frac{n}{4})+n\lg n, T(1)=1 \)

ans

\( a=3,\;b=4,\;f(n)=n\lg n, \; n^{\log_{4}3} \)
\( f(n)\geq n^{\log_{4}3}=n^{0.\dots } \)
By master theorem
\( f(n)=\Omega(n^{\log_{b}a+\varepsilon})\wedge\varepsilon > 0 \rightarrow T(n)=\Theta(f(n)) \)

\( f(n)= n\lg n=\Omega(n^{\log_43+\varepsilon}) \)
取\( \varepsilon=1-\log_43 \)
得
\( T(n)=\Theta(f(n))=\Theta(n\lg n) \)

exercise

\( T(n)=7T(\frac{n}{2})+n^3 \)

ans

\( a=7,\;b=2,\;f(n)=n^3,\;n^{\log_ba}=n^{\log_27} \)
\( f(n)=n^3> n^{\log_27} \)
\( n^3=f(n)=\Omega(n^{\log_27+\varepsilon}) \)
取\( \varepsilon=3-\log_27 \Rightarrow \varepsilon> 0 \)
\( af(\frac{n}{b})=7f(\frac{n}{2})\leq cf(n) \)
\( \Rightarrow 7\cdot \frac{n^3}{8}\leq cn^3 \Rightarrow c=\frac{7}{8} \Rightarrow c< 1 \)
By Master Theorem
\( T(n)=\Theta(f(n))=\Theta(n^3) \)

exercise

\( T(n)=3T(\frac{n}{2})+n^2\log n \)

ans

\( a=3,\; b=2,\; f(n)=n^2\log n,\; n^{\log_ba}=n^{\log_23}=n^{1.\dots } \)
\( n^2\log n= f(n) > n^{\log_23} \)
\( 3T(\frac{n}{2})\leq cf(n) \)
\( \Rightarrow 3(\frac{n^2}{4}\log\frac{n}{2}) \leq cn^2\log n \), 取\( c = \frac{3}{4} \Rightarrow c< 1\)
\( n^2\log n = f(n)=\Omega(n^{\log_23+\varepsilon}) \), 取 \( \varepsilon=2-\log_23 \Rightarrow \varepsilon > 0 \)
By Master Theorem
\( T(n)=\Theta(f(n))=\Theta(n^2\log n) \)