big-O
\( f(n)=O(g(n)) \)\( g(n) \) is asymptotically upper bound of \( f(n) \).
\( \exists c_0,n_0>0 \)
\( \rightarrow \forall n\geq n_0 \; (0\leq f(n)\leq c_0g(n)) \)
big-omega
\( f(n)=\Omega(g(n)) \)\( g(n) \) is asymptotically lower bound of \( f(n) \).
\( \exists c_0,n_0>0 \)
\( \rightarrow \forall n\geq n_0 \; (0\leq c_0g(n)\leq f(n)) \)
big-theta
\( f(n)=\Theta(g(n)) \)\( g(n) \) is asymptotically tight bound of \( f(n) \).
\( \exists c_0,c_1,n_0>0 \)
\( \rightarrow \forall n\geq n_0 \; (0\leq c_0g(n)\leq f(n)\leq c_1g(n)) \)
small-o
\( f(n)=o(g(n)) \)\( g(n) \) is asymptotically strict upper bound of \( f(n) \).
\( \forall c_0>0,\exists n_0>0 \)
\( \rightarrow \forall n\geq n_0 \; (0\leq f(n) < c_0g(n)) \)
small-omega
\( f(n)=\omega(g(n)) \)\( g(n) \) is asymptotically strict lower bound of \( f(n) \).
\( \forall c_0>0,\exists n_0>0 \)
\( \rightarrow \forall n\geq n_0 \; (0 \leq c_0g(n)< f(n)) \)
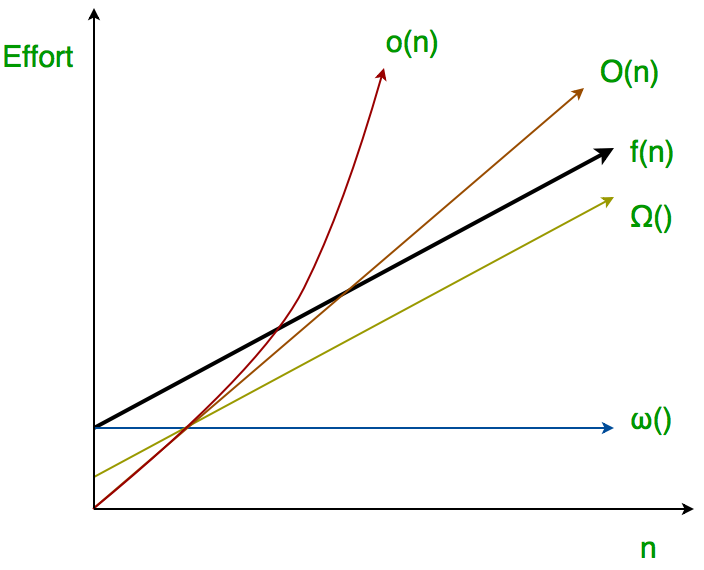
image reference
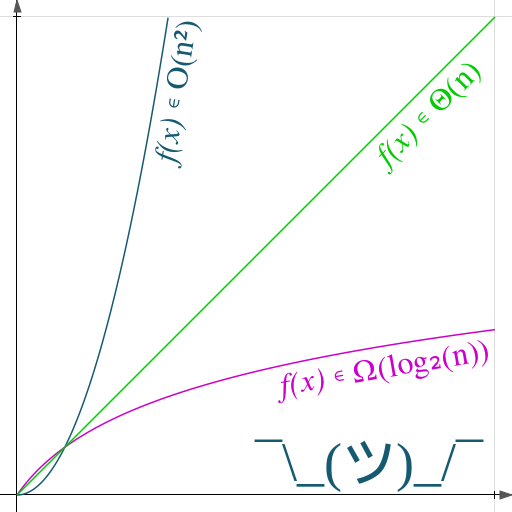
image reference